Implement regular expression matching with support for '.' and '＊' '.' Matches any single character. '＊' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

The function prototype should be: bool isMatch(const char ＊s, const char ＊p)

Some examples: isMatch("aa","a") → false isMatch("aa","aa") → true isMatch("aaa","aa") → false isMatch("aa", "a＊") → true isMatch("aa", ".＊") → true isMatch("ab", ".＊") → true isMatch("aab", "c＊a＊b") → true

这个题让人很是头疼啊，我卡了好久呢，首先要正确理解题意。 ＊可以匹配0或多个前面的字符，而 .可以匹配任意字符。那么看下面这个例子：
abc .＊ 看起来好像不匹配的样子，但其实不然。.＊ means repeating dot 0 or more times which actually can match any string.
greedy is not working since we don't know how many characters we should use '＊' to match. In this case, we need a backtracking strategy which allows us go back to previous successful state if current state fails. This naturally leads to a recursive solution.

1) If the next character of p is NOT ‘＊’, then it must match the current character of s. Continue pattern matching with the next character of both s and p.
2) If the next character of p is ‘＊’, then we do a brute force exhaustive matching of 0, 1, or more repeats of current character of p… Until we could not match any more characters.

//这个其实是错的,呵呵
    public boolean isMatch2(String s, String p){
        return helper(s, 0, p, 0);
    }
    private boolean helper(String s, int pos1, String p, int pos2){
        if (pos2 >= p.length()) return pos1 >= s.length();
        char c1 = p.charAt(pos2);
        char c2 = s.charAt(pos1);

        if (pos2 < p.length() - 1 && p.charAt(pos2 + 1) != '*'){
            return (c1 == c2 || (c1 == '.' && pos1 < s.length())) && helper(s, pos1 + 1, p, pos2 + 1);
        }
        while (c1 == c2 || (c1 == '.' && pos1 < s.length())){
            if (helper(s, pos1, p, pos2 + 2)) return true;
            pos1++;
        }
        return helper(s, pos1, p, pos2 + 2);
    }

This solution actually has O(2^n) worst case time complexity. To optimize it, we can easily come up with a DP solution which as the following diagram explains:

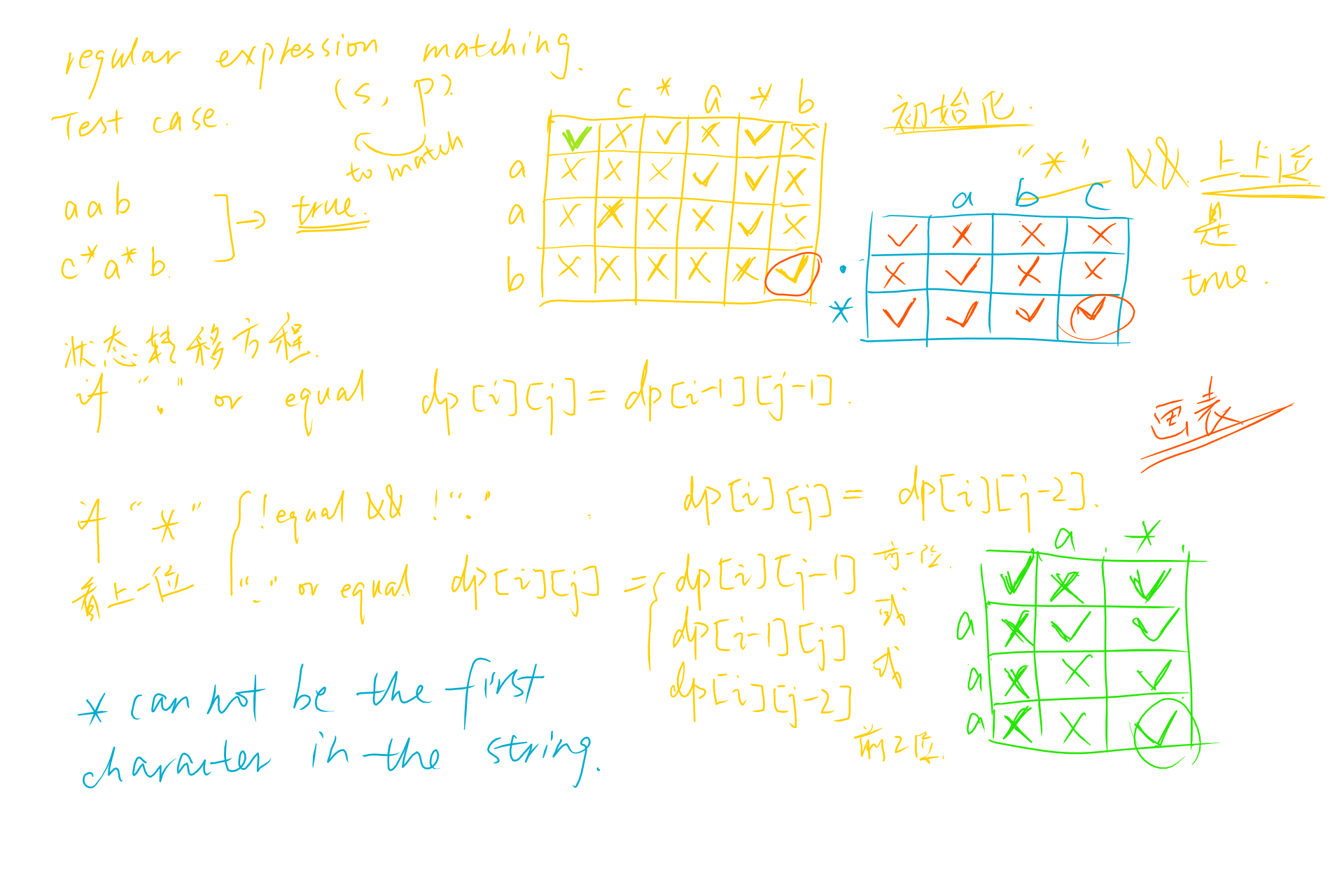
public boolean isMatch(String s, String p) {
        if (s == null || p == null) return false;
        int n = s.length(), m = p.length();
        boolean [][] dp = new boolean[n + 1][m + 1];
        dp[0][0] = true;
        for (int i = 1; i <= m; i++){
            if (p.charAt(i - 1) == '*' && dp[0][i - 2]){
                dp[0][i] = true;
            }
        }
        for (int i = 1; i <= n; i++){
            for (int j = 1; j <= m; j++){
                char curS = s.charAt(i - 1);
                char curP = p.charAt(j - 1);
                if (curS == curP || curP == '.'){
                    dp[i][j] = dp[i - 1][j - 1];
                }
                if (curP == '*'){
                    char preP = p.charAt(j - 2);
                    if (preP == curS || preP == '.'){
                        dp[i][j] = (dp[i - 1][j] || dp[i][j - 1] || dp[i][j - 2]);
                        /* dp[i - 1][j] -> match multiple
                        dp[i][j - 1] -> match 0
                        dp[i][j - 2] -> match 1

                        */
                    }else{
                        dp[i][j] = dp[i][j - 2];
                    }
                }
            }
        }
        return dp[n][m];
    }

This time complexity of this solution is O(NM), n and m is length of s and p separately.
以上。