236 Lowest common ancestor in tree

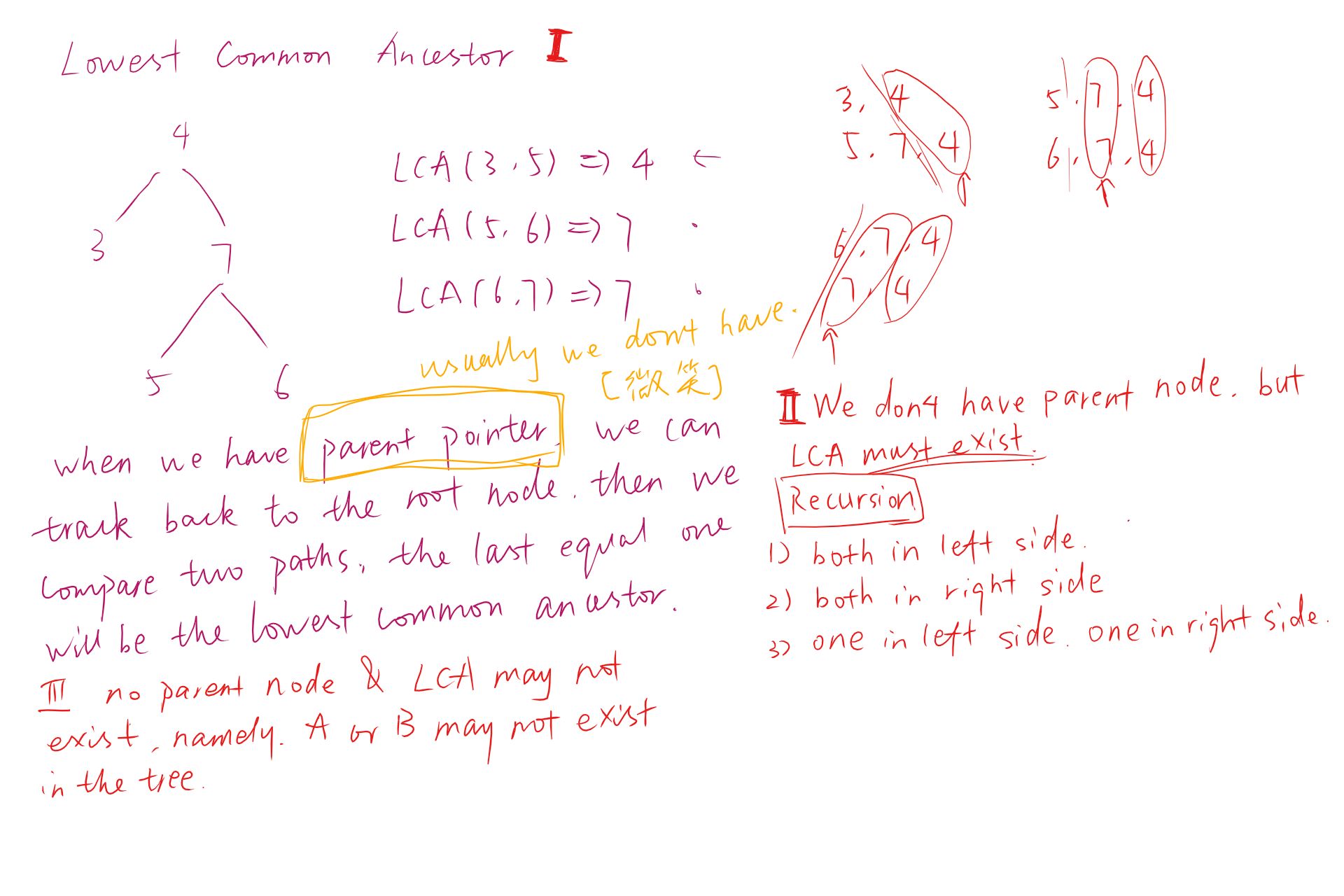
The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself). For the following binary tree:

 4
 / \
3 7
  / \
5  6
LCA(3, 5) = 4

LCA(5, 6) = 7

LCA(6, 7) = 7

This question has some variants, let's start from the easy one: 1) has parent node in TreeNode structure 2) Both A and B exist in the tree 3) A or B may not exist in the tree 4) the tree is not binary tree, it's n-ary tree For type 1, we can get path for both nodes first and then compare two paths from root until we find two nodes which are different. However, the optimal solution doesn't use extra space. It solved question in the following way:
If both nodes are at same level and if we traverse up using parent pointers of both nodes, the first common node in the path to root is lca. The idea is to find depths of given nodes and move up the deeper node pointer by the difference between depths. Once both nodes reach same level, traverse them up and return the first common node.

public TreeNode lca(TreeNode root, TreeNode p, TreeNode q){
  if (root == null) return root;
  int de1 = getDepth(p);
  int de2 = getDepth(q);
  int diff = de1 - de2;
  //q is deeper than p, swap these two
  if (diff < 0){
    TreeNode tmp = p;
    p = q;
    q = tmp;
    diff = -1 * diff;
  }
  while (diff-- != 0){
    p = p.parent;
  }
  while (p != null && q != null){
    if (p == q) return p;
    p = p.parent;
    q = q.parent;
  }
  return null;
}
private int getDepth(TreeNode n){
  int depth;
  while (n != null){
    depth++;
    n = n.parent;
  }
}

For type 2 and type 3, thinking process is like this: The last type is a little more complex. n-ary tree means each node may have multiple children rather than only two. In this case, we can write our program based on binary tree version's logic.

public TreeNode n-aryLCA(TreeNode root, TreeNode p, TreeNode q){
  if (root == null || p == root || q == root) return root;
  int counter = 0;
  TreeNode lca = null;
  for (TreeNode r : root.children){
    TreeNode tmp = n-aryLCA(r, p, q);
    if (!= null){
      counter++;
      lca = tmp;
    }
  }
  //equal to 2 means we found the two targets in two branches
  if (counter == 2) return root;
  return lca;
}

以上。