91 Decode Ways

A message containing letters from A-Z is being encoded to numbers using the following mapping:

'A' -> 1 'B' -> 2 ... 'Z' -> 26 Given an encoded message containing digits, determine the total number of ways to decode it.

For example, Given encoded message "12", it could be decoded as "AB" (1 2) or "L" (12).

The number of ways decoding "12" is 2.

The optimal solution is using dp, but this can also be solved by path-memorized dfs. dp solution diagram is like this:

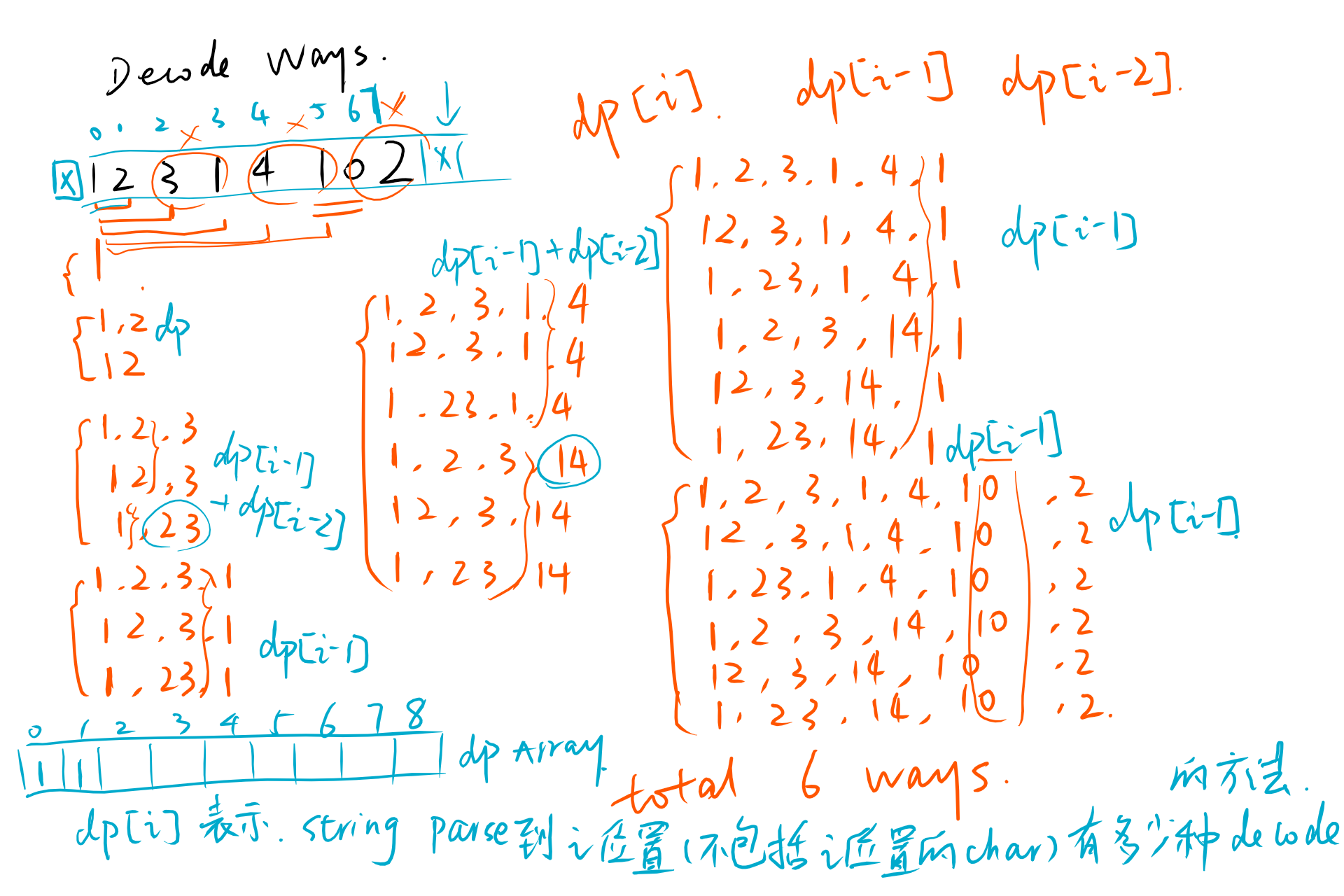
public int numDecodeWays(String s){
  if (s == null || s.length() == 0) return 0;
  int[] dp = new int[s.length() + 1];
  dp[0] = 1;
  dp[1] = s.charAt(0) == '0' ? 0 : 1;
  for (int i = 2; i <= s.length(); i++){
    int lastOne = Integer.parseInt(s.substring(i - 1, i));
    int lastTwo = Integer.parseInt(s.substring(i - 2, i));
    if (lastOne >= 1 && lastOne <= 9){
      dp[i] += dp[i - 1];
    }
    if (lastTwo >= 10 && lastTwo <= 26){
      dp[i] += dp[i - 2];
    }
  }
  return dp[s.length()];
}

dfs的思路的话就是这样的：

  public int numDecodings(String s) {
        if (s == null || s.length() == 0) return 0;
        Set<String> numbers = new HashSet<>();
        for (int i = 1; i <= 26; i++){
            numbers.add(String.valueOf(i));
        }
        return helper(new HashMap<Integer, Integer>(), 0, s, numbers);
    }
  private int helper(Map<Integer, Integer> map, int pos, String s, Set<String> numbers){
        Integer count = map.get(pos);
        if (count != null) return count;
        if (pos == s.length()) return 1;
        int numOfWays = 0;
        if (pos + 1 <= s.length() && numbers.contains(s.substring(pos, pos + 1))){
            numOfWays += helper(map, pos + 1, s, numbers);
        }
        if (pos + 2 <= s.length() && numbers.contains(s.substring(pos, pos + 2))){
            numOfWays += helper(map, pos + 2, s, numbers);
        }
        map.put(pos, numOfWays);
        return numOfWays;
    }

以上。